Current Projects
Mathematics of gene regulatory networks:
Everyone has seen the spaghetti diagrams of what genes interact with what others via some omics assay. At the other extreme is the Waddington landscape whose visual incarnation has assumed the status of a visual cliché. There is a lot of biological wisdom in Waddington’s metaphor, during development outcomes are strongly canalized, ie restricted to a few discrete outcomes. When dissected to the level of individual genes, it may look like spaghetti, but the noodles all cooperate to reinforce a small number of outcomes.
There happens to be an interesting mathematical abstraction of gene regulatory networks that goes under the rubric of Morse-Smale systems . These are flows (e.g. sets of differential equation) with a discrete number of ‘rest points’ and the property of structural stability (ie no change in topology of flows in an open neighborhood of parameters). This aligns very well with development, there is no chaos and poking an embryo a bit will not perturb its ultimate trajectory. In this context (+ some technical assumptions) Steve Smale in 1961 proved that the flow can be rewritten as a metric times the gradient of a potential ie.
Note this is equality, not ‘sort of similar to’. Thus, the dynamics defines a potential, or colloquially all life is downhill, so the Waddington metaphor becomes a theorem.
In Smale’s construction the rest points are ordered by the number of unstable directions, with the stable points at the bottom of the potential. This is a strong statement about dimensional reduction, the number of dimensions strictly necessary is the number of unstable eigenvectors at the rest point. Along with this theory is a proof that the only generic (accessed by tuning only one parameter) bifurcations necessary to interconvert two Morse-Smale systems on the same manifold are the familiar saddle-node, and the less articulated heteroclinic flip. This is a global bifurcation that reconnects the outset of a saddle. It’s not a local bifurcation that can be represented as the unfolding of a potential such as done in Thom’s catastrophe theory.
Note the familiar pitchfork bifurcation (as in the Ising model) is not in this list, since it requires a degeneracy between up and down states, so it‘s co-dimension two (ie realized by tuning two parameters). That may be easy to accomplish in a magnet, but in biology it's harder, and the burden of proof is on those who assume it.
The paper of Rand et al PNAS 2021 adds to the Smale construction by enumerating all topologically inequivalent two parameter phase spaces. It's a short list and an illuminating one is pasted in below…
This all seems too good to be true, since we are handed compact functional forms with which to fit any sort of developmental transitions. Where’s the catch? The theory is formulated for gene networks, implicitly intra cell. How do we handle many interacting cells, spatial patterns from reaction diffusion systems, mechanical interactions, and how do we parameterize in our compact functions specific genetic perturbation.
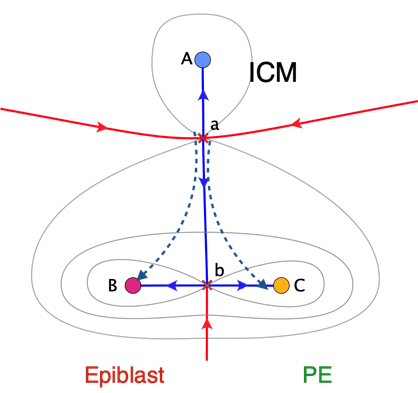
Examples of many cells interacting via long range Notch-Delta are given in Rand PNAS 2021. The system nicely illustrate the Smale hierarchy of rest points ordered by the number of unstable directions. The other example, under experimental study with the Hadjantonakis lab is the lineage separation of the inner cell mass in the mouse blastocyst into epiblast and primitive endoderm, involving 10’s of cells. Here the preferred model is a collective heteroclinic flip with a morphogen feedback represented as a time dependent spatially uniform mean field.
Turing systems are an interesting conundrum for Smale’s classification (Rand 2021), since the verbal description would seem to require the cross derivatives of the activator and inhibitor to be of opposite sign, hence not potential. As regards practicality, I would assert that no pattern of biological importance is described by a Turing system where there are many unstable modes. True the leopard needs its’ spots but their precise placement does not matter much. When we deal with Turing systems in a small domain with one or a few unstable modes, then a very nice potential description emerges for the unstable manifold of the saddle point that is the content of Turing’s model.
For the problem of fitting multiple genetic perturbations to a reduced dimensional model, we refer to our papers on the Vulva in C.elegans. This is a classical genetic system that is strongly canalized, so that a trained eye can place the division pattern of almost all mutants into one of three terminal fates. For this system multiple mutants in the Notch and EGF pathway were fit, with ostensible epistasis emerging from just the geometry. We believe that forcing many mutants into a compact representation will require some finesse that goes beyond proper mathematics, but will prove illuminating.
Experimental Collaborations (as of 8/2023)
With the lab of James Briscoe at the Crick Institute London we are fitting models for stem cell differentiation to various neuronal types in the spinal cord. This is a very interesting system since in the textbook cartoon, there is signaling from the roof plate (dorsal) and the floor plate (ventral), that collectively give rise to 11 subtypes along the DV axis. The strength of these systems is that the cellular environment can be controlled in time. The weakness is that some intracell signaling can not be controlled and is apt to be non native since the organization of the cells on the slide is random. Perhaps canalization remedies some of these problems, but some cell sorting and induced signals maybe part of the normal program. These differentiation protocols typically yield at most 50% of one population, which is a flag that all is not understood. The goal of the models is to predict a protocol adjusting levels and timing to induce a pure population.
Some years ago I collaborated with the lab of Kat Hadjantonakis at MSK (so literally a block from my office), to implement the gastrulation micropattern assay for the mouse embryonic stem cells. We continue to collaborate through shared postdocs on the blastocyst lineage decision, mentioned above, and visualizing some of the morphogens in live blastocysts.
The lab of Elly Tanaka in Vienna is well known for their studies of limb regeneration in salamanders (axolotl’s technically). This is a fascinating process in which terminally differentiated cells, dedifferentiate to recapitulate in part the normal developmental program that patterns the limb. Manipulations during regeneration can give rise to supernumerary digits and entire forearms (see her various reviews). The symmetry of the regenerated parts follows phenomenological rules with strong homologies with fly, that were already known to Bateson in the late 19th century (LINK HEeald). Regeneration is a challenging problem for those interested in pattern formation since the prepattern present during normal development is lacking.
Another focus of the Tanaka lab are neural cysts, that develop from single stem cells seeded in a 3D matrix. After induction of neural fates corresponding to the hindbrain along the AP axis the cysts express floor plate markers that intensify initially in salt and pepper configuration, and then aggregate into one or more compact regions. Intra-cyst communication is likely via BMP and its inhibitors. For me, this is an ideal system to develop geometric models of spatial structures in a context where the number of patterns is tightly limited.